Having struggled to create an accurate functional to describe molecules such as water for years, physicists have now turned their attention to how tools like ML can help with the task. In the process, DM21 is born. By Faraaz Akhtar
Water is perhaps our oldest friend, our most important resource. So important in fact, that we get excited anytime we find water on a planet—hoping that its presence there could also be an indication of life. As such, it makes sense that scientists continue to study it even now, using any and every tool available to them. However, the tool we discuss here—machine learning (ML)—is not just any tool; it easily surpasses the very essence of what our evolution consisted of—pattern processing [1].
But what more is there to know about water? Researchers believe that understanding the very detailed structure of water could help us give a molecular-level description of the physical properties of systems containing water. As a ubiquitous, polar molecule, water is relevant to every field of science from drug solubility to gas storage. As such, a deeper understanding of these systems could end up helping us in ways we may not be able to imagine. To do this, researchers looked to Density Functional Theory (DFT), a popular computational method used to calculate the electronic structure of atoms and molecules, through the exciting lens of machine learning. To properly appreciate this development, an understanding of the underlying theory is important.
Quantum physics arose as a consequence of experimental observations that showed that at extremely small scales, classical ideas of physics fail to describe occurring phenomena. More specifically, at these scales, particles exhibit wave-like behaviour, continuous values are suddenly quantized, and we introduce a demanded uncertainty into our reality. In order to make measurements, we then employ the use of a wavefunction, which contains all available information about a quantum system (such as position, momentum, and energy) [2]. This is usually done by substituting the wavefunction into the Schrödinger equation, where it is acted on by the Hamiltonian operator to give the total energy of the system. Attempts at having a fully calculable form of the Hamiltonian equation is where DFT comes in.
The Hamiltonian includes many terms that describe the behaviour of nuclei and electrons in the system. After simplifying the expression with some useful assumptions that cancel out some terms, the humble physicist is left with one particularly problematic term—the one describing electron-electron interactions. As the number of electrons in most chemically interesting systems is greater than one, simultaneously calculating every possible interaction is far too computationally heavy for most computers, let alone humans [3].
Nevertheless, all hope is not lost! A powerful bit of information that the wavefunction provides us with, is the probability of a particle being at a certain position. Consequently the probability of a number of electrons being at a particular set of coordinates can then be approximated. This leads very naturally to the concept of electron density [4].
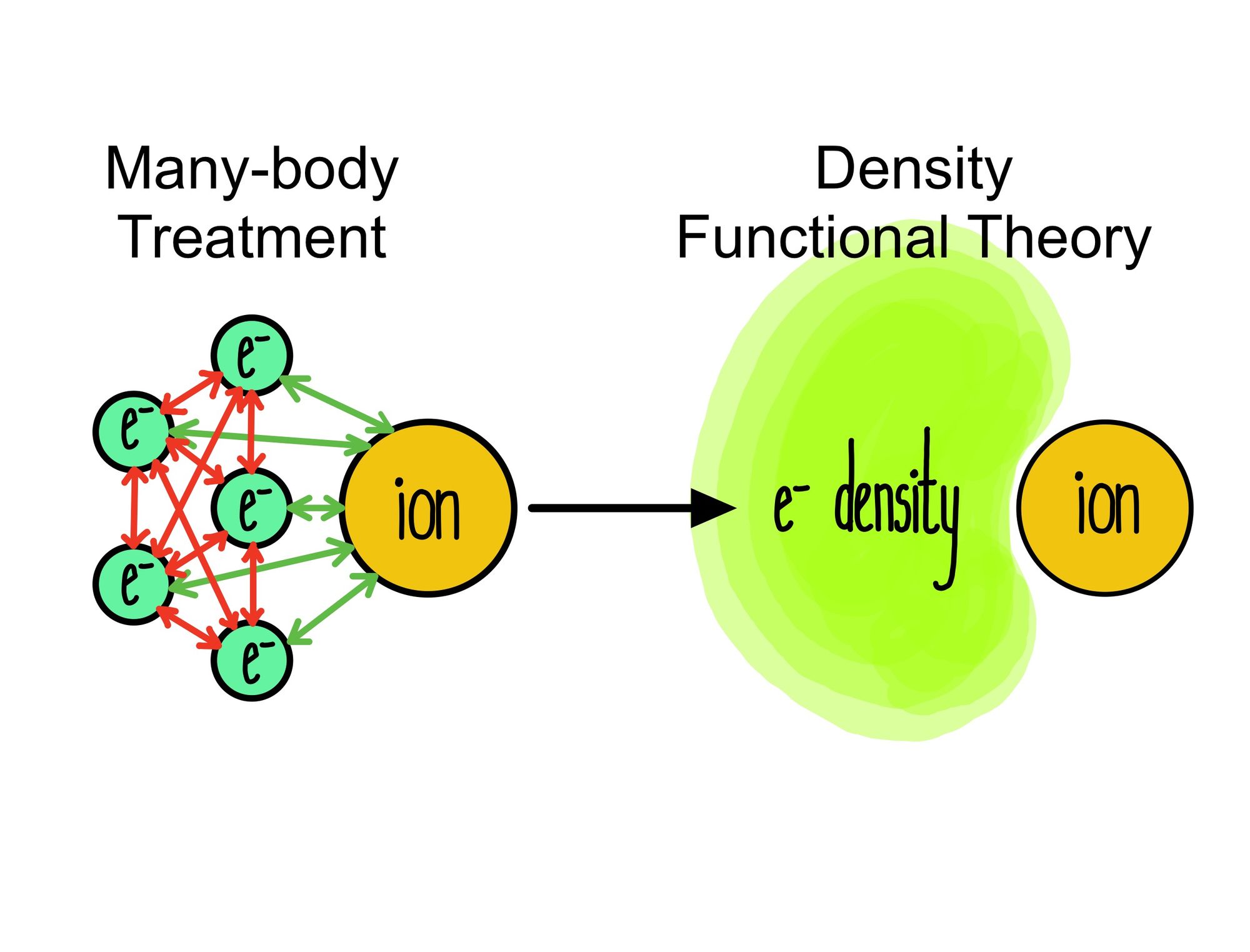
Physicists Pierre Hohenberg and Walter Kohn suggested that the energy of a system could be found through this electron density — one of two statements that now constitute the Hohenberg-Kohn theorem [5]. This is also exactly what DFT is: The ground state energy from the Schrödinger equation is a unique functional of electron density [6].
This functional — the link between the electron density and energy — is what physicists have struggled to describe accurately [7]. However, where there are patterns that are difficult for humans to determine, machines seem to thrive. This is exactly what makes machine learning such a powerful tool; the ability to take in an array with multiple features and run it through layers of some optimization function, allowing it to perform tasks that we humans may simply never see otherwise.
ML applications to DFT were first implemented as early as eleven years ago. By using a process known as kernel ridge regression (which is just a fancy term for a somewhat controlled regression) and training the model on accurate numerical calculations, an extremely accurate functional was found. However, its efficiency was limited to simple systems, like the one it was trained on.
There have been significant developments since 2012, the most exciting being a machine-learned functional based on an old human-designed functional. Called DeepMind 21 (DM21), it was trained on thousands of molecular structures, including simple systems with slight changes to the wavefunction. This allowed the functional to distinguish between similar systems, such as H2, H2+, and N2 — a definite step forward as strongly correlated molecular systems have always been difficult to tell apart [8]. Unfortunately, DM21 being great at predicting many molecular systems does not mean it has been very successful at predicting the properties of water. A study in 2022 showed that when applied to water under certain conditions, DM21 predicted a water that, instead of being a liquid, was more ice-like at room temperature [9].
Although frustrating, this is not necessarily a loss for the physicists trying to determine the structure of water. Both physics and machine learning are highly iterative processes and failure is embedded into the scientific method. If anything, we can be glad that DM21—which is almost two years old now—is bringing us ever closer to being able to identify patterns that we simply could not have predicted on our own.
References:
[1] Mattson MP. Superior pattern processing is the essence of the evolved human brain. Frontiers in Neuroscience [Internet]. 2014 Aug. [Accessed 27th September 2023]. Available from: <https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4141622/>
[2] Zyga L. Does the quantum wave function represent reality? [online] Phys.org. 2012 Apr. [Accessed 7 July 2023] Available from: <https://phys.org/news/2012-04-quantum-function-reality.html>
[3] Alhassid Group. The Nuclear Many-Body Problem. [online] Yale University. [Accessed 7 July 2023] Available from: <https://alhassidgroup.yale.edu/nuclear>
[4] S. Garcia-Granda, J.M. Montejo-Bernardo. X-RAY ABSORPTION AND DIFFRACTION: X-Ray Diffraction – Single Crystal. Encyclopedia of Analytical Science (Second Edition). Elsevier; 2005. p. 397-408. https://www.sciencedirect.com/science/article/abs/pii/B9780124095472005783
[5] Wolfram Koch, Max C. The Hohenberg-Kohn Theorems. A Chemist’s Guide to Density Functional Theory. Holthausen: Wiley-VCH; 2001. P. 33-36. https://onlinelibrary.wiley.com/doi/book/10.1002/3527600043
[6] Adams J.B. Bonding Energy Models. Encyclopaedia of Materials: Science and Technology (Second Edition)[online]. 2001: 763-767. [Accessed 16th October 2023] Available from: https://doi.org/10.1016/B0-08-043152-6/00146-7
[7] Adrienn Ruzsinszky, Lucian A. Constantin, Jianwei Sun, and Gábor I. Csonka. Some Fundamental Issues in Ground-State Density Functional Theory: A Guide for the Perplexed. J. Chem. 2009. 5 (4), 902-908. [Accessed Date: 7th July 2023] Available from: https://pubs.acs.org/doi/10.1021/ct800531s
[8] Pederson, R., Kalita, B. & Burke, K. Machine learning and density functional theory. Nat Rev Phys 4. 2022; [Date Accessed 7th July 2023] p. 357–358. Available from: https://doi.org/10.1038/s42254-022-00470-2
[9] Palos E, Lambros E, Dasgupta S & Paesani F. Density functional theory of water with the machine-learned DM21 functional. The Journal of Chemical Physics. 2022; [Date Accessed 27th September 2023]156(16):161103. https://doi.org/10.1063/5.0090862





